Ayala Zeta Luis
jueves, 25 de septiembre de 2008
martes, 23 de septiembre de 2008
PROYECTO DE LOGICA EN FLASH
SÁNCHEZ MORÁN JAVIER..................5 "B"
HERRERA SEGUNDO KELLY...............5 "B"
HERRERA SEGUNDO KELLY...............5 "B"
miércoles, 25 de junio de 2008
CASO2:
En este caso la variable angular se descompone en un múltiplo de 360° (vueltas enteras) más o menos, otro ángulo (agudo u obtuso), luego se eliminan las vueltas enteras:

Ejemplo: reducir al primer cuadrante
-tan765° = tan45°
-sen690° = sen330° = -sen30°
-cos1220° = cos 140° = -cos40°
-tan765° = tan45°
-sen690° = sen330° = -sen30°
-cos1220° = cos 140° = -cos40°
editado por eysenck gomez
CASO 1:
En este caso la variable angular se descompone en un múltiplo de 90° omenos otro ángulo agudo. Luego se usa el siguiente esquema:
Ejemplo: reducir al primer cuadrante
-sen(90° + x) = cos x
-tan(270° + x) = -cot x
-tan120° = -cot 30°
-sec240°=-csc 30°
-sec(3π/2 – x) = -csc x
-sen(90° + x) = cos x
-tan(270° + x) = -cot x
-tan120° = -cot 30°
-sec240°=-csc 30°
-sec(3π/2 – x) = -csc x
Ejemplo: reducir al primer cudrante
-tan(180° - x) = -tan x
-sen(360° - x) = -sen x
-sec300° = sec60°
-tan120° = -cot60°
-csc(2π – x) = -csc x
-tan(180° - x) = -tan x
-sen(360° - x) = -sen x
-sec300° = sec60°
-tan120° = -cot60°
-csc(2π – x) = -csc x
editado por eysenck gomez
Reducción al Primer Cuadrante
Reducir al primer cuadrante consiste en relacionar las razones trigonométricas de ángulos en posición estándar con las R.T de ángulos agudos (ángulos del primer cuadrante).
Casos de Reducción al primer Cuadrante
Para el estudio de reducción al primer cuadrante se presentan los siguientes casos:
CASO 1. cuando se trata de ángulos positivos, menores de una vuelta.
CASO 2. cuando se trata de ángulos positivos mayores de una vuelta.
CASO 3. cuando se trata de ángulos negativos.
editado por eysenck gomez
Casos de Reducción al primer Cuadrante
Para el estudio de reducción al primer cuadrante se presentan los siguientes casos:
CASO 1. cuando se trata de ángulos positivos, menores de una vuelta.
CASO 2. cuando se trata de ángulos positivos mayores de una vuelta.
CASO 3. cuando se trata de ángulos negativos.
editado por eysenck gomez
Determinación de los coterminales:
Los coterminales son obtenidos sumando a dicho ángulo un número entero de vueltas positivas o negativas.

Coterminales de 100° =
460°, 820°, 1180°
-260°, -620°, -980°
Propiedad de los coterminales:
Primera propiedad:
Si α y θ son coterminales se cumplirá que la diferencia es un número entero de vueltas

Segunda propiedad:
Si α y θ son coterminales se cumplirá que las razones trigonométricas de ambos ángulos son iguales.

Pero:
editado por eysenck gomez
Los coterminales son obtenidos sumando a dicho ángulo un número entero de vueltas positivas o negativas.

Coterminales de 100° =
460°, 820°, 1180°
-260°, -620°, -980°
Propiedad de los coterminales:
Primera propiedad:
Si α y θ son coterminales se cumplirá que la diferencia es un número entero de vueltas

Segunda propiedad:
Si α y θ son coterminales se cumplirá que las razones trigonométricas de ambos ángulos son iguales.

Pero:

editado por eysenck gomez
martes, 24 de junio de 2008
lunes, 16 de junio de 2008
Razones Trigonometricas de Angulos en Posicion Estandar
Ángulo en posicion estandar, canonica o normal:
Ángulos Cuadrantales:
Es aquel que tiene su superficie en el origen de coordenadas rectangulares y su lado y su lado inicial es el semieje "X" y su lado final puede estar en cualquiera de sus 4 cuadrantes (IC, IIC, IIIC, IVC).
Ángulos Cuadrantales:
Son aquellos angulos en posicion estandar cuyo lado final se ubica en los semiejes. Los angulos cuadrantes no pertenecen a ningun cuadrante.
editado por eysenck gomez; jhoel morales
LA CIRCUNFERENCIA
I. DEFINICION:
Una circunferencia es el lugar grométrico de todos los puntos que equidistan de un punto fijo, al punto fijo se le denomina centro y a la distancia constante se le llama radio.
II. ECUANCIONES DE LA CIRCUNFERENCIA:
Ecuacion Ordinaria:
Ecuacion Canónica:
Ecuacion General:
Se tiene:
(x - h)^2 + (y - k)^2 = r^2
Desarrolando:
x^2 - 2hx + h^2 + y^2 - 2hy^2 = r^2
Acomodando los términos:
x^2 + y^2 + (-2h)x + (-2k)y + (h^2+k^2-r^2) = 0
Haciendo un cambio de variable:
D = (-2h) ; E = (-2k) ; F = (h^2+k^2-r^2)
Reemplazando se tiene:
x^2 + y^2 + Dx + Ey + F = 0
Donde se deduce:
C(-D/2;-E/2)
r = raiz de:(D^2+E^2-4F)/2
Publicado por: Jhoel Morales
Una circunferencia es el lugar grométrico de todos los puntos que equidistan de un punto fijo, al punto fijo se le denomina centro y a la distancia constante se le llama radio.
II. ECUANCIONES DE LA CIRCUNFERENCIA:
Ecuacion Ordinaria:
Ecuacion Canónica:
Ecuacion General:
Se tiene:
(x - h)^2 + (y - k)^2 = r^2
Desarrolando:
x^2 - 2hx + h^2 + y^2 - 2hy^2 = r^2
Acomodando los términos:
x^2 + y^2 + (-2h)x + (-2k)y + (h^2+k^2-r^2) = 0
Haciendo un cambio de variable:
D = (-2h) ; E = (-2k) ; F = (h^2+k^2-r^2)
Reemplazando se tiene:
x^2 + y^2 + Dx + Ey + F = 0
Donde se deduce:
C(-D/2;-E/2)
r = raiz de:(D^2+E^2-4F)/2
Publicado por: Jhoel Morales
martes, 29 de abril de 2008
Ecuacion de la recta
Viene a ser aquellas expresiones que nos relacoina a las cordenadas rectangulares "x" e "y" de todos los puntos que estan en la recta.
Todo punto que esta en la recta debera cumplir con la ecuacion de dicha recta.

Ejem.:
3x + 4y + 1 = 0 ----> m = -(3/4)
2x - 3y + 1 = 0 ----> m = -(2/-3) ----> m = 2/3
Publicado por Jhoel Morales.
Todo punto que esta en la recta debera cumplir con la ecuacion de dicha recta.

Ejem.:
3x + 4y + 1 = 0 ----> m = -(3/4)
2x - 3y + 1 = 0 ----> m = -(2/-3) ----> m = 2/3
Publicado por Jhoel Morales.
lunes, 28 de abril de 2008
Propiedades
Propiedades
.1) Rectas paralelas (//)
Si: L1 // L2 =…………. m1=m2
.2) Rectas perpendiculares ( _l_ )
Si: L1 _l_ L2 =…….. m1 * m2 =-1
La cual implica que:
Si: m1= a/b =…… m2 = -b/a
Publicado por Javier Sánchez Morán
.1) Rectas paralelas (//)
Si: L1 // L2 =…………. m1=m2
.2) Rectas perpendiculares ( _l_ )
Si: L1 _l_ L2 =…….. m1 * m2 =-1
La cual implica que:
Si: m1= a/b =…… m2 = -b/a
Publicado por Javier Sánchez Morán
Ecuaciones pendientes – intercepta
Ecuaciones pendientes – intercepta
Esta ecuación se emplea cuando se conoce la pendiente a la recta y además su interfecto con el eje Y.
En esta ecuación se encuentra despejado la variable Y.

B – intercepto con el eje Y
Ejercicios:
2X + 3Y + 6 = 0
3Y = - 2X - 6
Y = - 2/3X - 2
Y = mx + b
m = - 2/3
b = -2
y = -2

3x - 4y +12 = 0
4y = 3x + 12
Y = 3/4 + 3
Y = mx + b
M = 3/4
B = 3

Publicado por Javier Sánchez Morán
Esta ecuación se emplea cuando se conoce la pendiente a la recta y además su interfecto con el eje Y.
En esta ecuación se encuentra despejado la variable Y.

B – intercepto con el eje Y
Ejercicios:
2X + 3Y + 6 = 0
3Y = - 2X - 6
Y = - 2/3X - 2
Y = mx + b
m = - 2/3
b = -2
y = -2

3x - 4y +12 = 0
4y = 3x + 12
Y = 3/4 + 3
Y = mx + b
M = 3/4
B = 3

Publicado por Javier Sánchez Morán
martes, 22 de abril de 2008
la recta
PRACTICA DIRIGIDA
1.- ¿Qué tipo de triangulo determina los puntos A(-2;-1) ; B (2,2) y C (-5,2)
2.- Calcular el punto medio del segmento cuyos extremos son los puntos (4;9) y (6;13)
3.- De la fig. Hallar “x + y”

4.- Si M(-3;5) es un punto que divide al segmento AB en la razón 4 : 1. Hallar las coordenadas de “A”, si B ( -2,2 )
5.-Dado el segmento AB donde A(4,-3), si su punto medio es (0,3). Hallar las coordenadas de B
6.- Hallar el perímetro del triangulo limitado por los puntos P(0,0); Q(25,0); R(9;12)
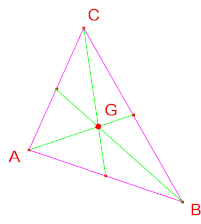
7.- Los vértices de un triangulo ABC son A(-5;1); B(1;6); C(7;4). Halle la distancia del baricentro del triangulo al vértice “A”.
8.- Señale la suma de las coordenadas del punto medio de un segmento cuyos extremos son los puntos A(7;-2) y B(3,-8)
9.- Si un punto A(0;y) equidista de los puntos B(4;2) y C(5,5). Halle la suma de las coordenadas del baricentro del triangulo de vértices A, B y C
10.- Sobre una recta se toman los puntos A, B, C y D de tal manera que B y C triscecan AD, si A(2;-3) y D(8;6. Halle las cordenadas de “B”
1.- ¿Qué tipo de triangulo determina los puntos A(-2;-1) ; B (2,2) y C (-5,2)
2.- Calcular el punto medio del segmento cuyos extremos son los puntos (4;9) y (6;13)
3.- De la fig. Hallar “x + y”

4.- Si M(-3;5) es un punto que divide al segmento AB en la razón 4 : 1. Hallar las coordenadas de “A”, si B ( -2,2 )
5.-Dado el segmento AB donde A(4,-3), si su punto medio es (0,3). Hallar las coordenadas de B
6.- Hallar el perímetro del triangulo limitado por los puntos P(0,0); Q(25,0); R(9;12)
7.- Los vértices de un triangulo ABC son A(-5;1); B(1;6); C(7;4). Halle la distancia del baricentro del triangulo al vértice “A”.
8.- Señale la suma de las coordenadas del punto medio de un segmento cuyos extremos son los puntos A(7;-2) y B(3,-8)
9.- Si un punto A(0;y) equidista de los puntos B(4;2) y C(5,5). Halle la suma de las coordenadas del baricentro del triangulo de vértices A, B y C
10.- Sobre una recta se toman los puntos A, B, C y D de tal manera que B y C triscecan AD, si A(2;-3) y D(8;6. Halle las cordenadas de “B”
Publicado por: [.Luis Ayala Zeta.]
lunes, 14 de abril de 2008
División de un segmento en una razón dada

P = (mA + nB) / (m + n)
Ejem:
*Hallar las coordenadas del punto que divide a un segmento cuyas coordenadas son A(1;2) y B(8;9), en una relación de 3 a 4.
RPTA: [3(8,9) + 4(1,2)] / 7 = (28; 35) / 7 = (4;5)
*el punto que divide a un segmento en la relación 2 a 3 es (8;4), si el un punto extremo es (4;3). Hallar el otro punto.
RPTA: 5P = (12;9) + (2x1 + 2y1) P = (14;23)

P = (mA + nB) / (m + n)
Ejem:
*Hallar las coordenadas del punto que divide a un segmento cuyas coordenadas son A(1;2) y B(8;9), en una relación de 3 a 4.
RPTA: [3(8,9) + 4(1,2)] / 7 = (28; 35) / 7 = (4;5)
*el punto que divide a un segmento en la relación 2 a 3 es (8;4), si el un punto extremo es (4;3). Hallar el otro punto.
RPTA: 5P = (12;9) + (2x1 + 2y1) P = (14;23)
Publicado por Eysenck Gómez
Distancia entre dos puntos 

D =√(x2-x1)2 + (y1-y2)2
Ejemplo: (tarea 07-03-08)
P(2;1) y Q(6;4)
D = √ (16 +9) = 5
P(3;4) y Q(-5;-1)
D = √ (81+16) = √97
P(-4;-2) y Q(6;7)
D = √ (100+81) = √181
P(3;-5) y Q(-1;1)
D = √ (16+36) = 2√13
P(1;5) y Q(-2;2)
D = √ (9+9) = 2√3
P(1;2) y Q(4;6)
D = √ (9+16) = 5
P(7;5) y Q(73;)
D = √ (0+4) = 2
Publicado por Eysenck Gómez


D =√(x2-x1)2 + (y1-y2)2
Ejemplo: (tarea 07-03-08)
P(2;1) y Q(6;4)
D = √ (16 +9) = 5
P(3;4) y Q(-5;-1)
D = √ (81+16) = √97
P(-4;-2) y Q(6;7)
D = √ (100+81) = √181
P(3;-5) y Q(-1;1)
D = √ (16+36) = 2√13
P(1;5) y Q(-2;2)
D = √ (9+9) = 2√3
P(1;2) y Q(4;6)
D = √ (9+16) = 5
P(7;5) y Q(73;)
D = √ (0+4) = 2
Publicado por Eysenck Gómez
publicado por: Javier Sánchez Morán

Ubicación de un punto
El punto se representa P(x ; y)
Absisa ________↑ ↑__________Ordenada
Grafico de plano cartesiano ubicado un punto
R: radio vector
Se cumple: R2 = x2 + y2
Un cuadrado tiene un lado de 10u de longitud. ¿cuáles son las coordenadas de sus vértices?
· Si uno de ellos está en el origen, dos de sus lados están a lo largo de las ordenadas y el otro vértice está en el IIC.
· Si su centro está en el origen y sus lados son paralelos a los ejes.
El punto se representa P(x ; y)
Absisa ________↑ ↑__________Ordenada
Grafico de plano cartesiano ubicado un punto
R: radio vector
Se cumple: R2 = x2 + y2
Un cuadrado tiene un lado de 10u de longitud. ¿cuáles son las coordenadas de sus vértices?
· Si uno de ellos está en el origen, dos de sus lados están a lo largo de las ordenadas y el otro vértice está en el IIC.
· Si su centro está en el origen y sus lados son paralelos a los ejes.
· RPTA: (0;0), (-10;0); (-10;10), (0;10)
· RPTA: (5;5), (-5;5), (-5;-5), (5;-5)
Publicado por Eysenck Gómez
GEOMETRIA ANALITICA
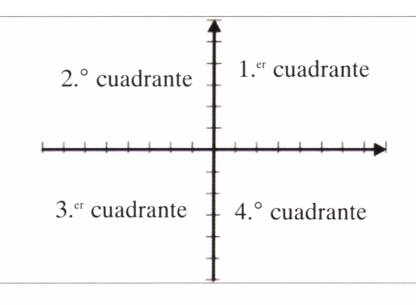
Sistema de coordenadas cartesianas
Es aquel sistema determinado por dos rectas que se cortan entre sí perpendicularmente y se encuentra en un mismo plano. A dicho plano se le denominado plano cartesiano.
O: origen de coordenadas
Eje x: eje de abcisas
Eje y: Eje de ordenadas
OA: semieje de ordenadas (+)
OC: semieje de abcisas (-)
OB: semieje de ordenadas (+)
OD: semieje de ordenadas (-)
Publicado por Eysenck Gómez
Es aquel sistema determinado por dos rectas que se cortan entre sí perpendicularmente y se encuentra en un mismo plano. A dicho plano se le denominado plano cartesiano.
O: origen de coordenadas
Eje x: eje de abcisas
Eje y: Eje de ordenadas
OA: semieje de ordenadas (+)
OC: semieje de abcisas (-)
OB: semieje de ordenadas (+)
OD: semieje de ordenadas (-)
Publicado por Eysenck Gómez
SILABO I BIMESTRE TRIGONOMETRIA
* Geometría analítica
- sistema de coordenadas rectangulares
- la recta
- la circunsferencia
- el elipse
- la parábola
*R.T de ángulos de cualquier magnitud
Publicado por Eysenck Gòmez
- sistema de coordenadas rectangulares
- la recta
- la circunsferencia
- el elipse
- la parábola
*R.T de ángulos de cualquier magnitud
Publicado por Eysenck Gòmez
martes, 1 de abril de 2008
INTRODUCCION
Suscribirse a:
Entradas (Atom)